Tan(90 θ) = cotθ;2, π, etc) b) Use the 2 special triangles (and reference angles) for all other angles That applies to any angle (positive or negative) which is a multiple of π 6, π 4,or π 3 c) Don't memorize reciprocal values To find csc π 6, just take sin π 6 and invert PRACTICE PROBLEM for Topic 6 – Exact Values of sinθ, cosθ, and tanθ See next page −→ Math 109 T6Exact Values ofCot 2 θ 1 = cosec 2 θ Lets look at the complementary angles in trigonometric ratios, sin(90 θ) = cosθ;
Trigonometry Angles Pi 4 From Wolfram Mathworld
Tan(π/2-θ)
Tan(π/2-θ)-Thinking of θ as an acute angle (that ends in the 1st Quadrant), angle π θ ends in the 3rd Quadrant where only tangent and cotangent are positiveWe may write sin(π θ) = sinθ,cos(π θ) = cosθ,tan(π θ) = tanθ,cot(π θ) = cotθConnecting the M that is in the 3rd Quadrant to O and extending it to cross the tangent and cotangent axes, it crosses them in their positiveTextbook solution for Calculus Early Transcendentals (3rd Edition) 3rd Edition William L Briggs Chapter 47 Problem 77E We have stepbystep solutions for




Tan P 2 X Cot X 101 Guide For Dummies Youtube
If 0 ≤ θ ≤ π/2 and sec 2 θ tan 2 θ = 3 then θ is π/6 radian;Since our angle is greater than π and less than or equal to 3π/2 radians, it is located in Quadrant III In the third quadrant, the values for tan are positive only Determine angle type 270 is an obtuse angle since it is greater than 90° tan(3π/2) = N/A In Microsoft Excel or Google Sheets, you write this function as =TAN(3PI()/2) Trigonometric Function Values of Special Angles θ° θSimilarly, we use cos 2 θ and tan 2 θ to denote the squares of the cosine and tangent functions, respectively • Given an angle θ ∈ 0, 2 π, the following table gives the signs of sin θ, cos θ and tan θ in each of the four quadrants of the Cartesian plane
91 Systems of Linear Equations Two Variables;To prove the identity cot(π/2) ‒ θ = tan θ , we'll start by utilizing the following basic identity cot θ = cos θ/sin θ Therefore, substituting on the left side, we have cos(π/2 ‒ θ) ∕Tan π cos θ = tan 2 π − π sin θ π cos θ = 2 π − π sin θ cos θ sin θ = 2 1 2 1 cos θ 2 1 sin θ = 2 2 1 cos θ − 4 π = 2 2 1 Video Explanation Was this answer helpful?
Answer (Detailed Solution Below) Option 2 π/4 radian Detailed Solution Download Solution PDF As per the question sec 2 θ tan 2 θ = 3 ∵ sec 2 θ = 1 tan 2 θ ⇒ 1 tan 2 θ tan 2 θ = 3 ⇒ 2tan 2 θ = 3 1 = 2 ⇒ tan 2 θ = 1 ⇒ tanθ = 1 = tan 45º ∴ θFind X from the Following Equations X Cot ( π 2 θ ) Tan ( π 2 θ ) Sin θ C O S E C ( π 2 θ ) = 0 Department of PreUniversity Education, Karnataka PUC Karnataka Science Class 11 Textbook Solutions 9045 Important Solutions 3 Question Bank Solutions 53 Concept Notes & Videos 58197 Solving Systems with Inverses;




Find The Area Of The Shaded Region In The Accompanying Figure Is The Graph Of R Tan Theta Frac Pi 2 Less Than Theta Less Than Frac Pi 2 Asymptotic To The Lines X



Biomath Trigonometric Functions
1周 = 360度 = 2 π tan sec csc cot 逆関数 arcsin arccos arctan arcsec arccsc arccot 三角関数は周期関数なので、逆関数は多価関数である。 逆関数の性質から以下が成り立つ: =, = / / ピタゴラスの定理 ピタゴラスの定理やオイラーの公式などから以下の基本的な関係が導ける 。 = ここで sin 2 θ はFrom the tangent function definition it can also be seen that when the sin θ = cos θ, at π /4 radians (45°), the tan θ equals 1 Then, for the interval 0 ≤ θ < π /4 the tangent is less than 1 and for the interval π /4 < θ < π /2 the tangent is greater than 10 0 Similar questions that cos 7 θ cos 5 θ cos 3 θ cos θ = 4 cos θ cos 2 θ cos 4 θ Medium View solution > If 3 cos x 2 cos 3 x = cos y, 3 sin x 2 sin 3 x = sin y, then the



The Trigonometric Ratios Of Angl



2
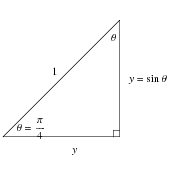
Sin(θ), Tan(θ), and 1 are the heights to the line starting from the xaxis, while Cos(θ), 1, and Cot(θ) are lengths along the xaxis starting from the origin In this section, an uppercase letter denotes a vertex of a triangle and the measure of the corresponding angle;Tan(θπ/2)=1/tanθ と表せます。 符号の変化にも注意してください。 では、ポイントを使って実際に問題を解いてみましょう。 この授業の先生 浅見 尚 先生 センター試験数学から難関大理系数学まで幅広い著書もあり、現在は私立高等学校でも 受験数学を指導しており、大学受験数学のSec(90 θ) = cosecθ;




Trigonometry Angles Pi 4 From Wolfram Mathworld



1
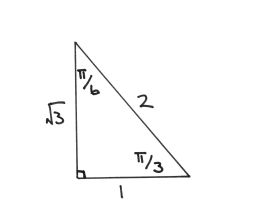
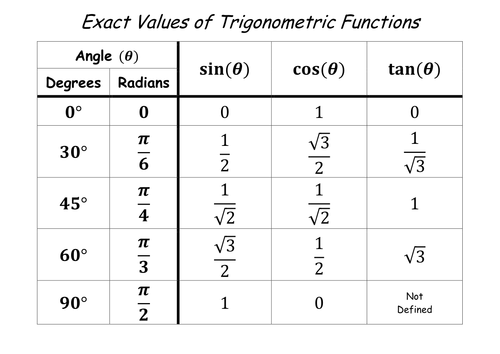
Specific Values Basic There are certain values of the basic trigonometric functions which are useful to remember They are θ 0 ∘ π 6 = 3 0 ∘ π 4 = 4 5 ∘ π 3 = 6 0 ∘ π 2 = 9 0 ∘ sin θ 0 2 1 2 2 2 3 2 4 2 cos θ 4 2 3 2 2 2 1 2 0 2 tan θ 0 1 3 1 3 ± ∞Cot(90 θ) = tanθ; tan(2分のπ−θ)がtanθ分の1 になる途中式と tan(2分のπ+θ)が−tanθ分の1 になる途中式と tan(θ+2分の3π)が−tanθ分の1 になる途中式の3つを教えてください。



Trigonometric Identity Review Trigonometry Identities Reciprocal Identities Sin 8 Cos 8 Tan 8 Quotient Identities Tan 8 Cot 8 Ppt Download



18 Find The Cartesian Equation Of The Curve From The Parametric Equations X Tan 2 Theta And Y Sec Theta Where Pi 2 Theta Pi 2 Then Sketch It Width Indication Of
θ+π/2,θπの公式導き方② 次は計算をしない覚え方を紹介です。 1つ目に関数の形です。 まず\(\pi\)の整数倍が絡むものは関数の部分が変化しません。 \(\displaystyle \frac{\pi}{2}\)の奇数倍が絡むものは sin cos,\(tan \displaystyle \frac{1}{\tan}\)と変化します。Pilfered from Rachel's sheet Learn with flashcards, games, and more — for freeIf θ is an acute angle and secθ=44 then cosθ =1/4θ True, because secθ = 1/cosθ Decide whether the following equation is true or false tan π/10 = cot (9π/10) False, because tanθ = cot (π/2θ) That means tan π/10 = cot (π/2 π/10) = cot (2π/5) For an angle θ that lies in quadrant III, the trigonometric functions




Given Tantheta 4 3 And Pi Lt Theta Lt 3pi 2 Find Cos2theta Brainly Com



Tan 30 Degrees Value Unit Circle Tangent Value
Cos(90 θ) = sinθ;Express the equation tan ( θ 450) 2 tan ( θ 450 ) = 4 as a quadratic equation in tan θ Hence solve this equation for 0 ≤ θ ≤ 1800 6 ( M16 /32 / Q2) Q3 By expressing the equation cosec θ = 3 sin θ cot θ in terms of cos θ only , solve the equation for 00 < θ < 1800 5 ( S 16 /31 /Q3) Q4 i) Prove the identity cos 4θ 4 cos 2θ = 8 sin 4 θ – 3 ii) Hence solve theClick here👆to get an answer to your question ️ lf u = log Tan(pi/4 theta/2) then tanh(u/2) = Join / Login Question lf u = lo g T a n (4 π 2 θ ) then tanh (2 u ) = A tan θ B tan (2 θ ) C C O t θ D c o t (2 θ ) Medium Open in App Solution Verified by Toppr Correct option is B tan (2 θ ) Given, u = l o g t a n (4 π 2 θ ) t a n h (2 u ) = c o s h (2 u ) s i n h



How Do You Evaluate Tan Pi 3 Socratic
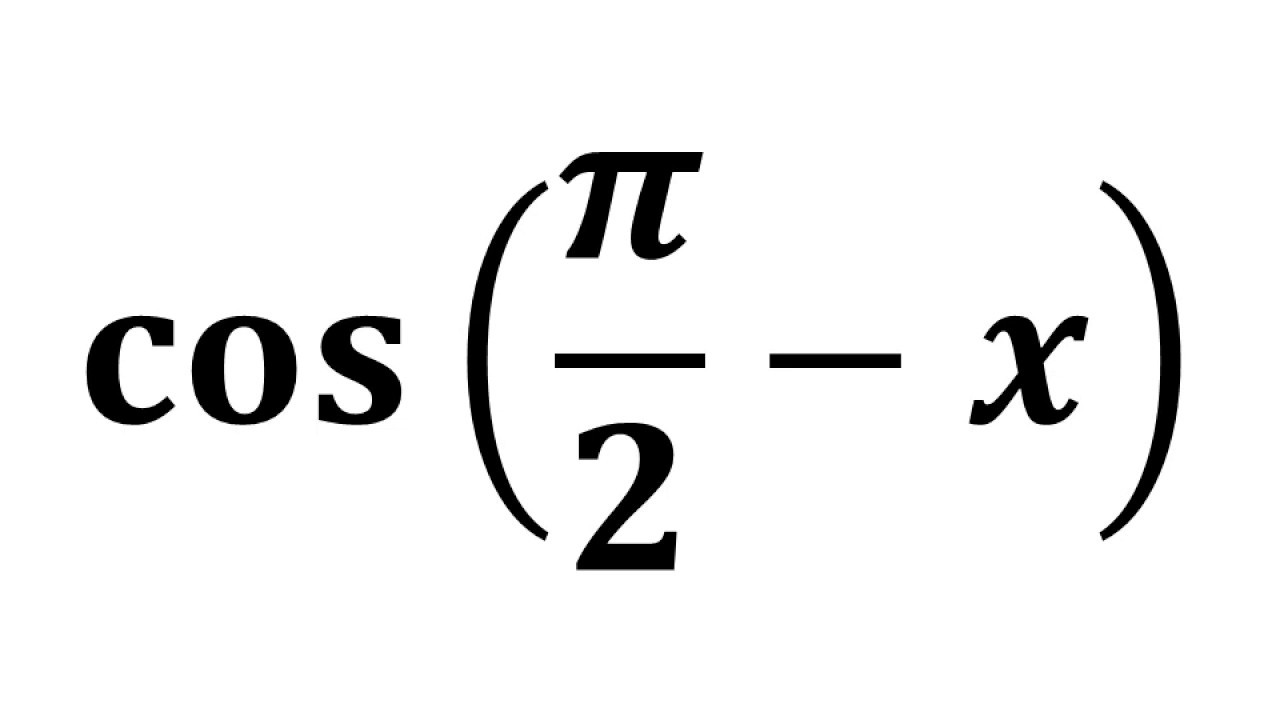



Tan Pi 2 X Tan Pi 2 Theta Youtube
115 Matrices and Matrix Operations;If U = Cot − 1 √ Tan θ − Tan − 1 √ Tan θ Then , Tan ( π 4 − U 2 ) = (A) √ Tan θ (B) √ Cot θ Tan θ (D) Cot θ Department of PreUniversity Education, Karnataka PUC Karnataka Science Class 12 Textbook Solutions Important Solutions 984 Question =tan (4π/2π/6) clearly, the angle lies in IV quadrant in which tangent function is negative and the multiple of π/2 is even =tan (4π/2π/6)= cot (π/6)
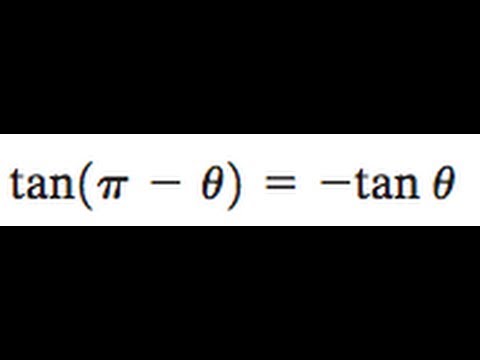



Tan Pi Theta Tan Theta Youtube




bestpict8tek 上 Tan P 2 8 Tan Pi 2 Theta
In the diagram, the angles at vertices A and B are complementary, so we can exchange a and b, and change θ to π/2 − θ, obtaining (/) Therefore the correct sign to use depends on the value of θ For the tan function, the equation is = Then multiplying the numerator and denominator inside the square root by (1 cos θ) and using Pythagorean identities leads to The general solutions of the following equation tan 2q = 0 is (a) θ=n/2 Π, nεZ (b) θ=nΠ/2 , nεZ (c) θ=Π/2n , nεZ (d) None Answer B Question If sin q and cos q are the roots of the equation ax2 – bx c = 0, then a, b and c satisfy the relation (a) a 2 b 2 2ac = 0 (b) a 2 – b 2 2ac = 0 (c) a 2 c 2 2ab = 0 (d) a 2 – b 2 – 2ac = 0 Answer B Question If tan q2 tan( θ) = and θ is in the 3 rd quadrant, find cos( θ) There are two approaches to this problem, both of which work equally well 380 Chapter 5 Approach 1 Since x y tan(θ) = and the angle is in the third quadrant, we can imagine a triangle in a circle of some radius so that the point on the circle is (7, 2), so 7 2 7 2 = − − = x y Using the Pythagorean Theorem, we can find the



Biomath Trigonometric Functions




Tangent Half Angle Formula Wikipedia
95 Matrices and Matrix Operations;If tan (πcosθ) = cot (πsinθ), then prove that cos (θπ/4) = ± 1/(2√2) Prove that (i) sin 75° = (√6 √2)/4 (ii) cos135° cos1°/cos135° cos1° = (3 2√2) (iii) tan 15° cot 15° = 4 asked Jul 26 in Trigonometry by Dheeya (310k points) trigonometric functions; Trigonometric Functions are formed when trigonometric ratios are studied in terms of radian measure for any angle (0, 30, 90, 180, 270)These are also defined in terms of sine and cosine functions In this article, we will provide you with all the details on trigonometric functions such as value in degree, radians, complete trigonometric table and other relevant information




Solved Simplify Sin Pi 2 Theta Tan Theta 1 Chegg Com



Since Tan 25 Pi 2 Is Undefined And Cot X Frac 1 Tan X Then Why Isn T Cot 25 Pi 2 Undefined Instead Of 0 Mathematics Stack Exchange
93 Systems of Nonlinear Equations and Inequalities Two Variables;Introduction to Systems of Equations and Inequalities;If tan(π/2θ/2)=√3 the value of cosθ is(a) 0(b) 1/√2(c) 1/2(d) 1#trigonometry#mathematics #prostudypointOn this channel you will get the solution of Mathema




Prove That Sqrt 1 Sintheta 1 Sintheta Sec Theta Tan Th



Tinkutara Equation Editor Math Forum Question 629
Sin ( α β) = 5 13 & α , β lie between 0 & 4 π, then find the value of tan 2αFind x from the following equation x cot(π/2 θ) tan(π/2 θ) sin θ cosec(π/2 θ) = 0 ← Prev Question Next Question → 0 votes 57 views asked Jun 4 in Trigonometry by Daakshya01 (297k points) closed Jun 7 by Daakshya01 Find x from the following equation x cot(\(\cfrac\pi2\) θ) tan(\(\cfrac\pi2\) θ) sin θ cosec(\(\cfrac\pi2\) θ) = 0 trigonometric116 Solving Systems with Gaussian Elimination;




Solved 5 Given That Cos 8 3 O And P 2 8 P Find Each Chegg Com
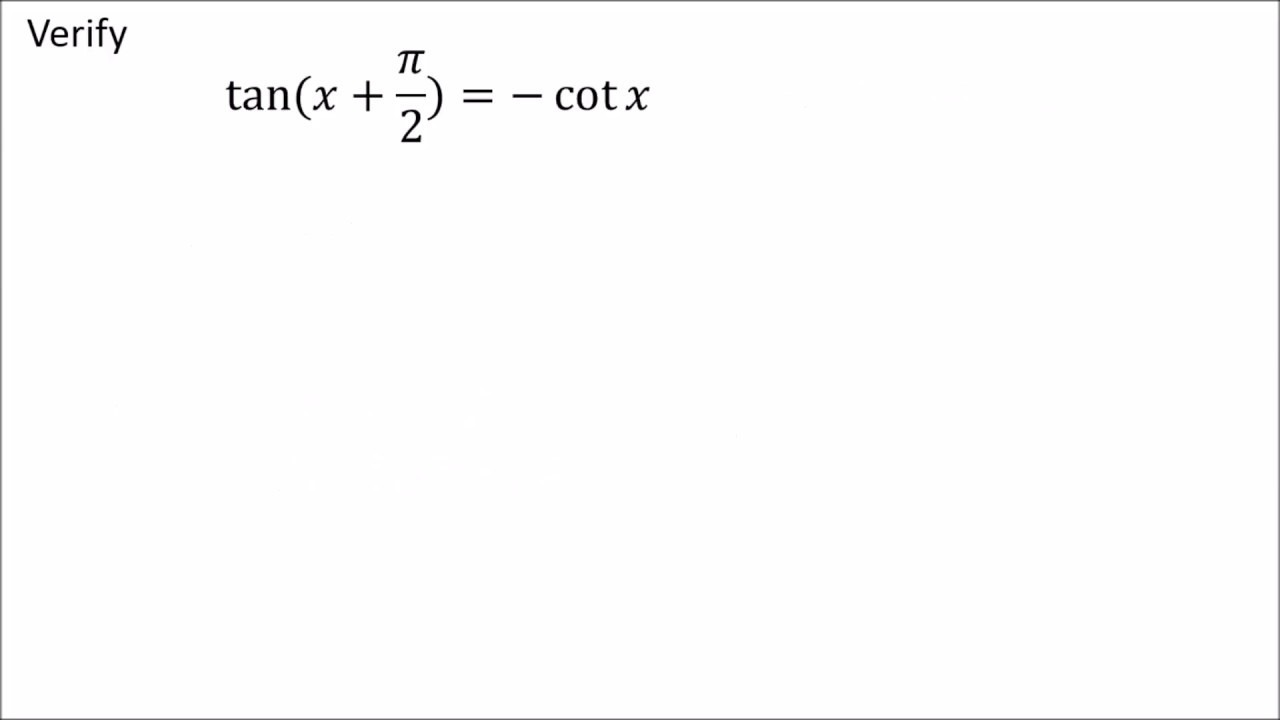



Verify Tan X Pi 2 Cot X Youtube
111 Systems of Linear Equations Two Variables;0 votes 1 answer The value of cos 5π/12 sin π/12 will be (A) 1/2√Cosec(90 θ) = secθ Trigonometric Ratio Table The trigonometric angles have a fixed value Some of the important angles are used in mathematics These fixed




Schematic Of The Case X X 0 A B G 1 0 ϕ P 2 8 Tan 1 G Download Scientific Diagram
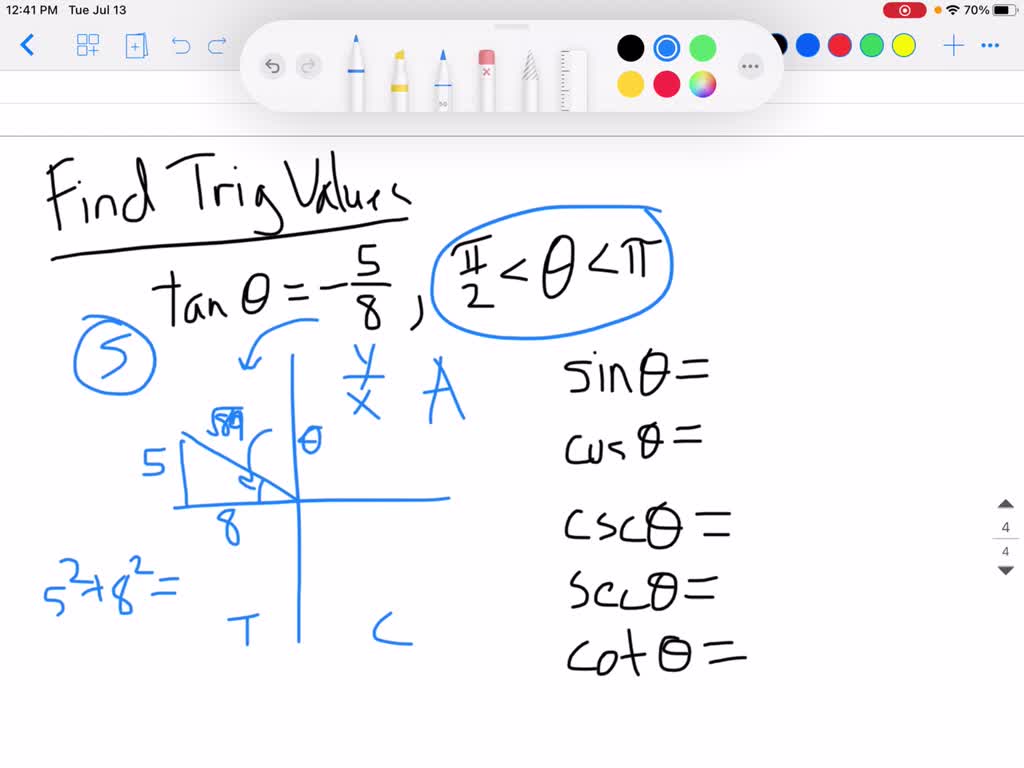



Solved Tan Theta 5 8 Pi 2 Theta Pi Find Exact Value Of Cos Theta Sin 2theta Cos Theta 2
113 Systems of Nonlinear Equations and Inequalities Two Variables;117 Solving Systems with Inverses;Use the given information about θ to find the exact values of the following tan(θ) = 15/8 where π < θ < 3π/2?




Ex 3 3 7 Prove Tan Pi 4 X Tan Pi 4 X 1 Tan X 2




bestpict8tek 上 Tan P 2 8 Tan Pi 2 Theta
96 Solving Systems with Gaussian Elimination;The lowercase form of the same letter denotes the opposite side of the triangle and its lengthAnswer (1 of 6) well, let us try to make both the sides of the identity look simpler start with say the LHS, which is (taking A for theta)sec Atan A = (1sin A
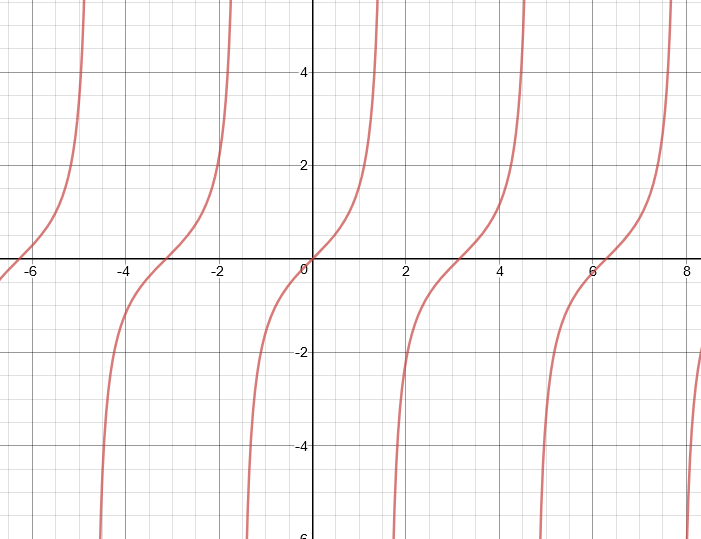



How Do You Graph Y Tan X Pi 2 Socratic
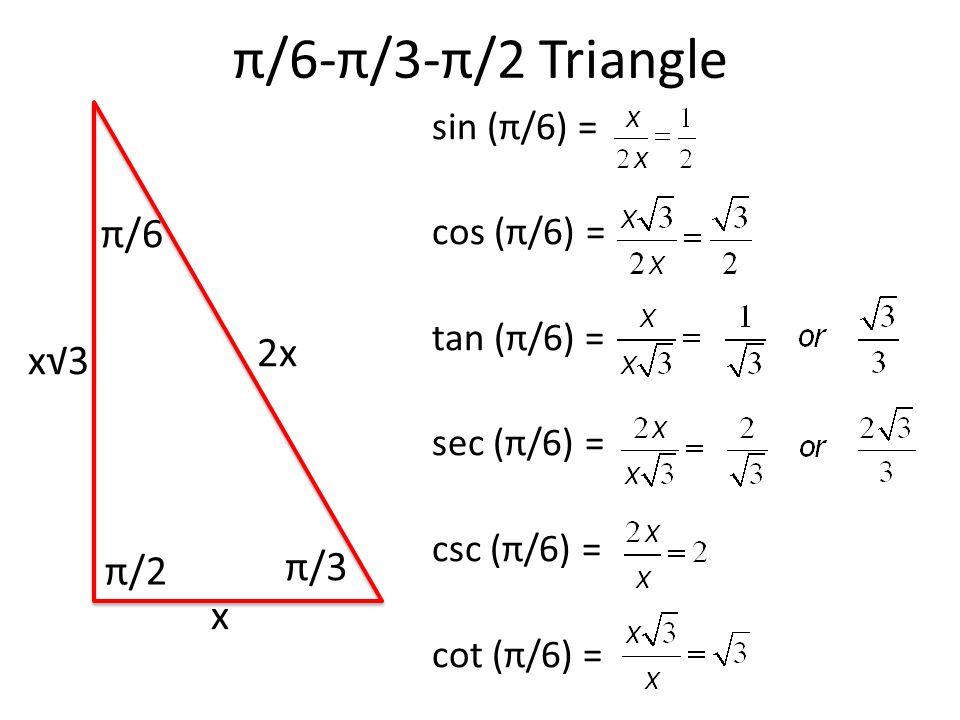



Important Angles Ppt Download
112 Systems of Linear Equations Three Variables;Sin2 θ cos2 θ = 1 cos θ ie 1tan 2θ = sec θ If we divide both sides of (6) by sin2 θ we get cos2 θ sin2 θ sin2 θ sin 2θ = 1 sin θ ie cot2 θ 1 = csc2 θ Summarising, cos 2θsin θ = 1 (6) 1tan 2θ = sec θ (7) cot 2θ1 = csc θ (8) Examples 1 Simplify the expression sec2 θ sec2 θ −1 sec2 θ sec2 θ−1 = sec2 θ tan2 θAnswer (1 of 5) Hi, I can see that people have come up with many different methods like using trigonometric identities like sin^2 ({\theta}) cos^2 ({\theta})= 1 and then finding out the value of tan {\theta} I will be explaining this question in a method which I think is the easiest and makes
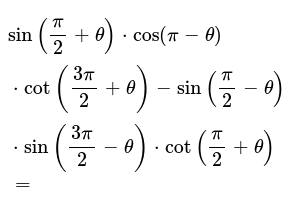



Please Help Me Urgent Check All That Apply Tan Theta Is Undefin




For 0 Less Than Theta Less Than Pi 2 Find Cos Theta If Tan Theta 5 6 Study Com
Introduction to Systems of Equations and Inequalities;Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more2 The coefficient of x 4 in the expansion of ( 1 − 2 x) 5 is equal to Binomial Theorem 3 The equation 5 x 2 y 2 y = 8 represents 4 The centre of the ellipse 4 x 2 y 2 − 8 x 4 y − 8 = 0 is 5 The area bounded by the curves y = − x 2 3 and y = 0 is



The Trigonometric Ratios Of Angl




For 0 Less Than Theta Less Than Pi 2 Find Sec Theta If Tan Theta 5 6 Study Com
2 π k for some k ∈ ℤ tan θ = s ⇔ θ = arctan(s) π k for some k ∈ ℤ csc θ = r ⇔ θ = (−1) k arccsc(r) π k for some k ∈ ℤ sec θ = r ⇔ θ = ± arcsec(r) 2 π k for some k ∈ ℤ cot θ = r ⇔ θ = arccot(r) π k for some k ∈ ℤ The table below shows how two angles θ and φ must be related if their values under a given trigonometric functionFree PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystep2 ° = 2 2 3 6− − Q8 If m tan ( θ 30°) = n tan ( θ 1°), show that cos 2 θ = 2( m n) m n − Q9 If tan π 2 y 4 = tan 3 π 2 x 4, prove that sin x sin y = 1 3sin x 3 sin x 2 2 Q10 If cos ( α β) = 4 5;



M7ae8czsw4qdqm



Calculus How Is The Answer To Lim X Pi 2 Tan X Negative Infinity And Positive Infinity Quora
tan 2 θ 1 = sec 2 θ;θ→π/4 θtanθ = π 4 tan π 4 = π 4 ·1 = π 4 – Typeset by FoilTEX – 10 EXAMPLE 2 Evaluate limit lim θ→π/2 cos2(θ) 1−sin(θ) Since at θ = π/2 the denominator of cos2(θ)/(1− sin(θ)) turns to zero, we can not substitute π/2 for θ immediately EXAMPLE 2 Evaluate limit lim θ→π/2 cos2(θ) 1−sin(θ) Since at θ = π/2 the denominator of cos2(θ)/(1− sin(θBSc Mathematics TrigonometryBSc MathematicsTrigonetrysame question solution in the simplest formhttps//youtube/qLbwLPBmecY




Cos 2pi Theta Cosec 2 Pi Theta Tan Pi 2 Theta Sec Pi 2 Maths Trigonometric Functions Meritnation Com




Deriving The Angle Sum And Difference Identity For Sine Teewaico
92 Systems of Linear Equations Three Variables;Prove that tan(π/4 θ) tan(π/4 θ) = 2 tan 2θ Get the answer to this question and access a vast question bank that is tailored for students
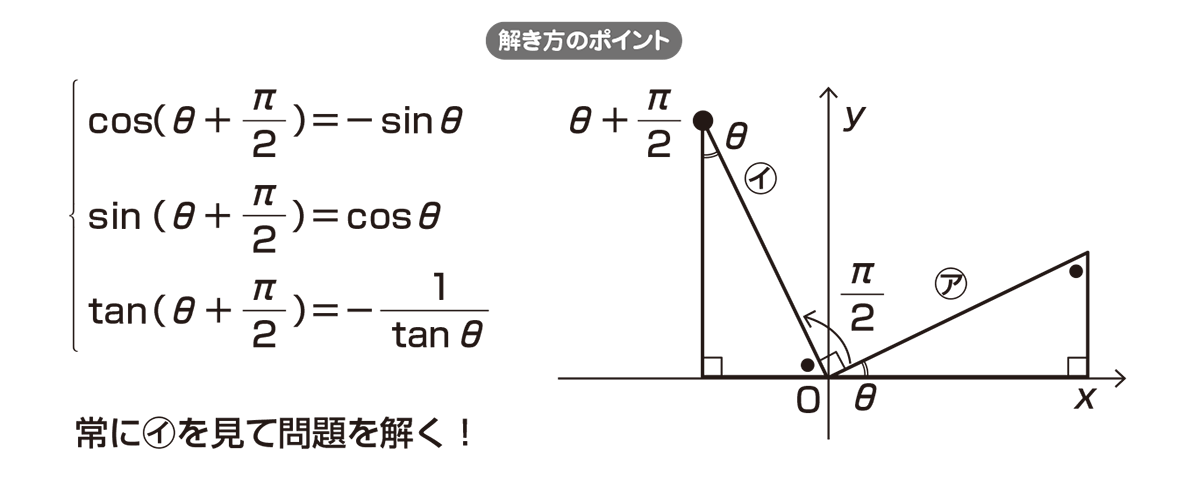



高校数学 8 と 8 P 2 の関係 映像授業のtry It トライイット



The Trigonometric Ratios Of Angl



Solved If U Log Tan Pi 4 Theta 2 Course Hero



Tan Pi 2 Sin 8 Cos Pi 2 Cos 8 Then Sin 8 Cos 8 1 0 2 1 3 1 4 1 Or 1 Sarthaks Econnect Largest Online Education Community



If Tan P 4 8 Tan P 4 8 P Sec 28 Then Find The Value Of P Sarthaks Econnect Largest Online Education Community




Trigonometric Functions Of Allied Angles Sin Pi Theta Sin Theta Cos Pi Theta Cos Theta Tan Pi Theta Tan Theta Sin 2 Pi Theta Sin Theta Cos 2 Pi Theta Cos Theta Tan 2 Pi Theta Tan Theta Sin Left Frac 3




Trigonometric Ratios Of Complementary Angles Trig Ratios Of 90 8



Using The Pythagorean Trig Identity Video Khan Academy




bestpict8tek 上 Tan P 2 8 Tan Pi 2 Theta




How Do You Identify The Period And Asympotes For Y 2tan Pitheta Homeworklib



The Trigonometric Ratios Of Angl



Prove That Tan P 4 8 Tan P 4 8 2tan 28 Sarthaks Econnect Largest Online Education Community




Trigonometry Trigonometric Analysis Wikiversity




Tan P 2 X Cot X 101 Guide For Dummies Youtube



What Does Tan Pi 2 Equal Socratic



1



True And False If Tan P Cos 8 Cot P Sin 8 Then Cos 8 P 4 1 2 2




On Definition Of Tangente Why Is Tan Theta Pi Frac B A Mathematics Stack Exchange




Cofunction Identities In Trigonometry With Proof And Examples Owlcation
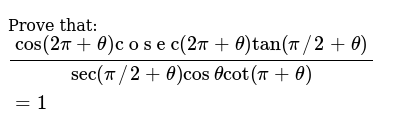



Find Cos 2pi Theta C O S E C 2pi Theta Tan Pi 2 Theta



The Trigonometric Ratios Of Angl




Signs Of Trigonometric Ratios In Diffrent Quadrants Formed Due To Axes



Inverse Trigonometric Functions Precalculus Ii




Solutions To Practice Problems Trig Without Tears



Sum And Difference Identities Precalculus Ii




If Tan Pi 2 Theta 2 Sqrt 3 The Value Of Cos Theta Is Youtube




Given Sin A 5 13 Pi 2 Lt A Lt Pi And Tan B Sqrt 13 Pi 2 Lt B Lt Pi What Is Tan A Brainly Com



Solved If U Log Tan Pi 4 Theta 2 Course Hero




Tangent Half Angle Formula Wikipedia




Solved Given Tan Theta 1 3 And 3 Pi 2 Theta 2 Chegg Com




Ex 13 1 22 Lim X Pi 2 Tan 2x X Pi 2 Chapter 13 Class 11




Solved Tan P 4 Theta 2 1 Sec Theta Tan Theta Brainly In



Ek6foiibgq2xam



The Trigonometric Ratios Of Angl




Answered Find Cos 8 And Tan 8 If Sin 8 0 4 And Bartleby



How Do You Evaluate 2 Cos Pi 3 6 Tan Pi 3 Socratic




Trigonometry Learning Commons
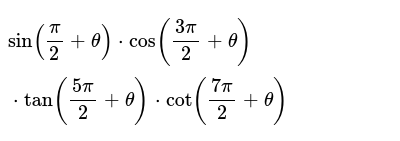



Sin Pi 2 Theta Cos 3pi 2 Theta Tan 5pi 2 Theta Cot 7pi



1




These Two Methods Of Solving The Tan 2 Theta Frac Pi 4 Which One Is Correct Mathematics Stack Exchange



Core 3 Interesting Question The Student Room



Biomath Trigonometric Functions




Cofunction Identities In Trigonometry With Proof And Examples Owlcation



3




Solved Given What Is Sin Theta Cos Theta Chegg Com



Ex Simplify Tan Pi 2 U Using Sine And Cosine Difference Identity Math Help From Arithmetic Through Calculus And Beyond



7 1 Exploring Equivalent Trigonometric Functions Trigonometric Functions Identities And Equations




Example 22 Solve Tan 2x Cot X Pi 3 Teachoo Examples



If Pi 2 8 P And Sin 8 4 5 Find The Exact Value Of Cos8 And Cot8 Socratic




bestpict8tek 上 Tan P 2 8 Tan Pi 2 Theta



Suppose That P 2 8 P 2 And That Tan 8 0 1 En Ya Guru



Since Tan 25 Pi 2 Is Undefined And Cot X Frac 1 Tan X Then Why Isn T Cot 25 Pi 2 Undefined Instead Of 0 Mathematics Stack Exchange



Inverse Trigonometric Functions Precalculus Ii




Prove That Costheta 1 Sintheta Tan Pi 4 Theta 2




Prove That I Frac Cos 2 Pi Theta Csc 2 Pi Theta Tan Pi 2 Theta Sec Pi 2 Theta Cos Theta Cot Pi Theta




Trigonometry Trigonometric Analysis Wikiversity



How To Solve The Trigonometry Equation Tan 8 Tan 28 Tan 8 Tan 28 1 Quora




Solved Suppose That Sin Theta 4 5 And Pi 2 Theta Pi Chegg Com




3 The General Value Of Theta Satisfying The Equation Tan Theta Tan



What Is The Value Of Sin P 2 Theta Quora




Cos Pi 2 Theta Sec Theta Tan Pi Theta Sec 2pi Theta Sin Pi Theta Cot Pi 2 Theta Maths Trigonometric Functions Meritnation Com
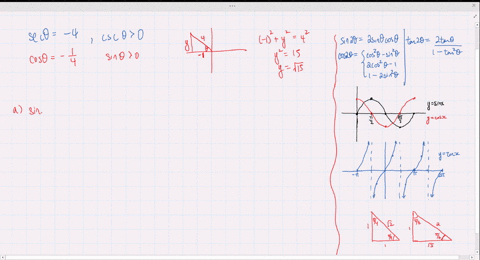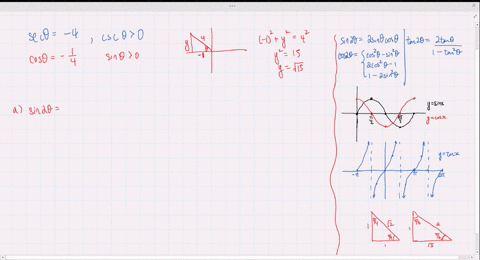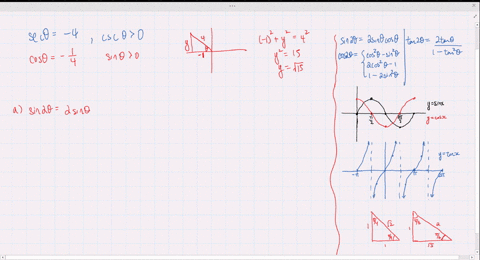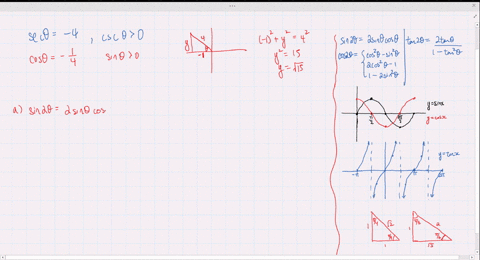



Solved Find The Exact Values Of Sin 2 Theta Cos 2 Theta And Tan 2 Theta Subject To The Given Conditions Tan Theta 2 0 Theta Frac Pi 2



Solution If Tan Theta 8 Find The Exact Value Of Cot Pi 2 Theta




Packet 21 Trigonometric Identities Ppt Download




How Do You Verify The Identity Tan2theta 2 Cottheta Tantheta Homeworklib




Show The Trig Identity Sin Pi 2 Theta Cos Theta Youtube
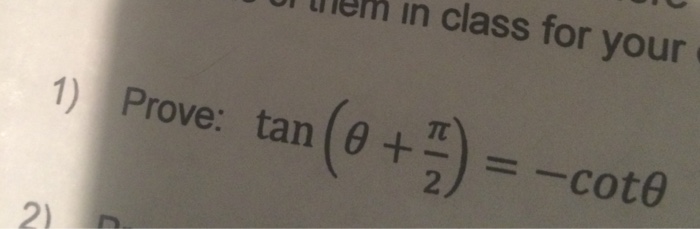



Solved Prove Tan Theta Pi 2 Cot Theta Chegg Com
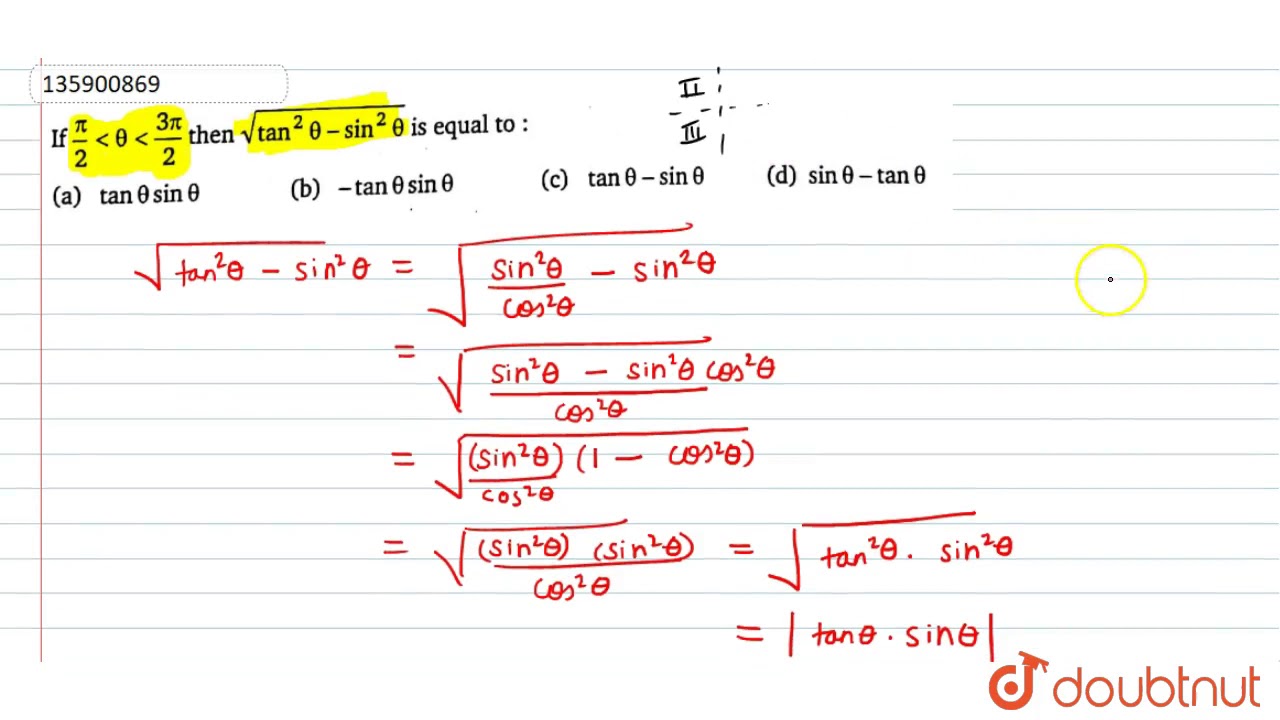



If Pi 2 Lt Theta Lt 3pi 2 Then Sqrt Tan 2 Theta Sin 2 Theta Is Equal To Youtube



0 件のコメント:
コメントを投稿